

The key difference between a mathematical expression and an equation is the presence of an an equals sign. So, for example, 2 + 3[5 − 4 · 2], x2 + 2x − 3, and x + 2y + 3 are mathematical expressions (two of which contain variables), while 3 + 2(7 − 3) = 11, x +3=4, and 3x = 9 are equations. Note that each of the equations contain an equals sign, but the expressions do not. Next we have the definition of a solution of an equation.
A solution of an equation is a numerical value that satisfies the equation. That is, when the variable in the equation is replaced by the solution, a true statement results.
Substitute 3 for x in the given equation and simplify. \[ \begin
Substitute 23 for y in the given equation and simplify. \[ \begin
The number 7 is the only solution of the equation x + 2 = 9. Similarly, 7 is the only solution of the equation x = 7. Therefore x + 2 = 9 and Answer: No. x = 7 have the same solution sets and are equivalent.
By inspection, the equation x 2 = x has two solutions, 0 and 1. On the other hand, the equation x = 1 has a single solution, namely 1. Hence, the equations x 2 = x and x = 1 do not have the same solution sets and are not equivalent.
There are many operations that will produce equivalent operations. In this section we look at two: addition and subtraction.
Adding the same quantity to both sides of an equation does not change the solution set. That is, if \[a = b,\nonumber \] then adding c to both sides of the equation produces the equivalent equation \[a + c = b + c.\nonumber \]
Let’s see if this works as advertised. Consider the equation x − 4=3. By inspection, 7 is the only solution of the equation. Now, let’s add 4 to both sides of the equation to see if the resulting equation is equivalent to x − 4 = 3. \[ \begin
It is also a fact that subtracting the same quantity from both sides of an equation produces an equivalent equation.
Subtracting the same quantity from both sides of an equation does not change the solution set. That is, if \[a = b,\nonumber \] then subtracting c from both sides of the equation produces the equivalent equation \[a − c = b − c.\nonumber \]
Let’s also see if this works as advertised. Consider the equation \[ x + 4 = 9.\nonumber \] By inspection, 5 is the only solution of the equation. Now, let’s subtract 4 from both sides of the equation to see if the resulting equation is equivalent to x + 4 = 9. \[ \begin & & <> & < \text < The given equation. >>> \\ & & <> & < \text < Subtract 4 from both sides of the equation. >>> \\ & & <> & < \text < Simplify both sides of the equation. >>>\end\nonumber \] The number 5 is the only solution of the equation \(x = 5\). Thus, the equation \(x = 5\) is equivalent to the original equation \(x + 4 = 9\) (they have the same solutions).
When solving equations, observe the following rules to neatly arrange your work: 1. One equation per line. This means that you should not arrange your work like this: \[ x+3=7 \quad x+3-3=7-3 \quad x=4\nonumber \] That’s three equations on a line. Rather, arrange your work one equation per line like this: \[ \begin x+3 &=7 \\ x+3-3 &=7-3 \\ x &=4 \end\nonumber \] 2. Add and subtract inline. Don’t do this: \[ \begin x -7 & = & 12 \\ +7 & & + 7 \\ \hline x & = & 19 \end\nonumber \] Instead, add 7 to both sides of the equation “inline.” \[ \begin x-7 &=12 \\ x-7+7 &=12+7 \\ x &=19 \end\nonumber \]
When we give the wrapped gift to our cousin, he politely unwraps the present, “undoing” each of our three steps in inverse order.
This seemingly frivolous wrapping and unwrapping of a gift contains some deeply powerful mathematical ideas. Consider the mathematical expression \(x+ 4\). To evaluate this expression at a particular value of x, we would start with the given value of x, then
Suppose we started with the number 7. If we add 4, we arrive at the following result: 11.
Now, how would we “unwrap” this result to return to our original number? We would start with our result, then
That is, we would take our result from above, 11, then subtract 4, which returns us to our original number, namely 7.
Two extremely important observations:
The inverse of addition is subtraction. If we start with a number x and add a number a, then subtracting a from the result will return us to the original number x. In symbols,
\[x + a − a = x.\nonumber \]
The inverse of subtraction is addition. If we start with a number x and subtract a number a, then adding a to the result will return us to the original number x. In symbols,
\[x − a + a = x.\nonumber \]
Solve \(x − 8 = 10\) for x.
To undo the effects of subtracting 8, we add 8 to both sides of the equation.
Therefore, the solution of the equation is 18.
Check
To check, substitute the solution 18 into the original equation.
The fact that the last line of our check is a true statement guarantees that 18 is a solution of x − 8 = 10.
Solve \(x + 5 = 12\) for x.
Answer
Solve \(11 = y + 5\) for y.
To undo the effects of adding 5, we subtract 5 from both sides of the equation.
Therefore, the solution of the equation is 6.
Check
The fact that the last line of our check is a true statement guarantees that 6 is a solution of 11 = y + 5.
Solve \(y - 8 = 11\) for y.
Answer
The solution of a word problem must incorporate each of the following steps.
Let's give these requirements a test drive.
Four more than a certain number is 12. Find the number.
In our solution, we will carefully address each step of the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. We can satisfy this requirement by simply stating “Let x represent a certain number.”
2. Set up an Equation. “Four more than a certain number is 12” becomes
3. Solve the Equation. To “undo” the addition, subtract 4 from both sides of the equation.
4. Answer the Question. The number is 8.
5. Look Back. Does the solution 8 satisfy the words in the original problem? We were told that “four more than a certain number is 12.” Well, four more than 8 is 12, so our solution is correct.
12 more than a certain number is 19. Find the number.
Answer
Amelie withdraws $125 from her savings account. Because of the withdrawal, the current balance in her account is now $1,200. What was the original balance in the account before the withdrawal?
In our solution, we will carefully address each step of the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. We can satisfy this requirement by simply stating “Let B represent the original balance in Amelie’s account.”
2. Set up an Equation. We can describe the situation in words and symbols.
3. Solve the Equation. To “undo” the subtraction, add 125 to both sides of the equation.
4. Answer the Question. The original balance was $1,325.
5. Look Back. Does the solution $1,325 satisfy the words in the original problem? Note that if Amelie withdraws $125 from this balance, the new balance will be $1,200. Hence, the solution is correct.
Fred withdraws $230 from his account, lowering his balance to $3,500. What was his original balance?
Answer
The perimeter of a triangle is 114 feet. Two sides of the triangle measure 30 feet and 40 feet, respectively. Find the measure of the third side of the triangle.
In our solution, we will carefully address each step of the Requirements for Word Problem Solutions.
1. Set up a Variable Dictionary. When geometry is involved, we can create our variable dictionary by labeling a carefully constructed diagram. With this thought in mind, we draw a triangle, then label its known and unknown sides and its perimeter.
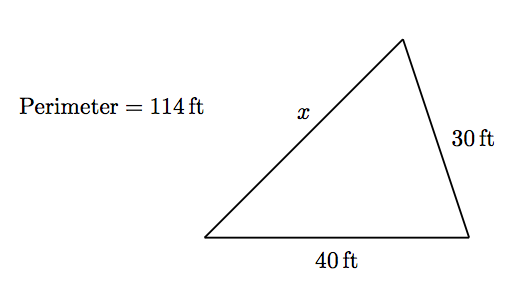
The figure makes it clear that x represents the length of the unknown side of the triangle. The figure also summarizes information needed for the solution. 2. Set up an equation. We know that the perimeter of a triangle is found by finding the sum of its three sides; in words and symbols,
Simplify the right-hand side by adding 30 and 40; i.e., \(30 + 40 = 70\).
\[ 114 = x + 70\nonumber \]
3. Solve the Equation. To “undo” adding 70, subtract 70 from both sides of the equation.
4. Answer the Question. The unknown side of the triangle is 44 feet.
5. Look Back. Does the solution 44 feet satisfy the words of the original problem? We were told that the perimeter is 114 feet and two of the sides have length 30 feet and 40 feet respectively. We found that the third side has length 44 feet. Now, adding the three sides, 30+ 40+ 44 = 114, which equals the given perimeter of 114 feet. The answer works!
The perimeter of a quadrilateral is 200 meters. If three of the sides measure 20, 40, and 60 meters, what is the length of the fourth side.
Answer
In Exercises 1-12, which of the numbers following the given equation are solutions of the given equation? Support your response with work similar to that shown in Examples 1 and 2.
1. x − 4 = 6; 10, 17, 13, 11
2. x − 9 = 7; 17, 23, 19, 16
3. x + 2 = 6; 5, 11, 7, 4
4. x + 3 = 9; 6, 9, 7, 13
5. x + 2 = 3; 8, 1, 4, 2
6. x + 2 = 5; 10, 3, 6, 4
7. x − 4 = 7; 12, 11, 18, 14
8. x − 6 = 7; 13, 16, 20, 14
9. x + 3 = 4; 8, 4, 2, 1
10. x + 5 = 9; 5, 11, 7, 4
11. x − 6 = 8; 17, 21, 14, 15
12. x − 2 = 9; 11, 14, 12, 18
In Exercises 13-52, solve the given equation for x.